Linear Phase Portraits: Matrix Entry
The type of phase portrait of a homogeneous linear autonomous system -- a companion system for example -- depends on the matrix coefficients via the eigenvalues or equivalently via the trace and determinant.
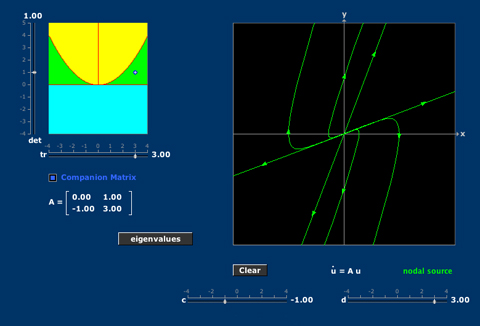 The type of phase portrait of a homogeneous linear autonomous system -- a companion system for example -- depends on the matrix coefficients via the eigenvalues or equivalently via the trace and determinant.
The type of phase portrait of a homogeneous linear autonomous system -- a companion system for example -- depends on the matrix coefficients via the eigenvalues or equivalently via the trace and determinant.
19 Responses to “Linear Phase Portraits: Matrix Entry”

the demo of phase plane and phase trajetories are very interesting and easy to understand for the system of differential equation. Thank for your demo program.
Why can't the top rows in the companion matrix be altered? Totally worthless.
The Companion matrix is defined to have top row [0 1].
Thank you very much for sharing this app. It helps a lot in the qualitative understanding of the solutions.
Thank you for this app. It was very useful to see the behavior of a system from a change in its matrix. If you creates an app to plot nonlinear systems, please tell me.
Great App!
Have you looked at Vector Fields?
For the companion matrix:
0 1
-2 2.5
The Mathlet arrives at the two real eigenvalues:
λ1=1.25
λ2=1.25
But the eigenvalues should be complex, not real:
λ1≈1.25+0.66i
λ2≈1.25−0.66i
Seems like a bug.
Thank you Hanson for pointing this out. I think it has been fixed.
Why is the top left element in the matrix now fixed to be 0? Like the old way
This is the meaning of "companion matrix." You can adjust the top row by deselecting [companion matrix].
Thank you very much for sharing this app. I am going to use it in a lecture in a few minutes. 😉
How did it go, Diego?
Shouldn't the diagrams be different if t^2 - 4delta = 0 depending on in the matrix is diagonalisable or not?
Yes ... and they are! Perhaps you have [companion matrix] checked: companion matrices with repeated eigenvalues are never diagonalizable.
I can now understand how this works! really interisting and I now see things way more clear!
Great, Joan. What was the AHA moment?
What software runs this Mathlet ? It's nice !
Consider the matrix [ -1 1 ; 2 -2 ] (first row is [-1 1] and the second row is [2 -2]).
This has rank 1 and the phase portrait is degenerate, as the Mathlet says.
All the points on the line x=y are 0s of the vector field, and all points not on the line
are attracted to some point on the line, and the Mathlet labels these orbits (rays) OK.
But the line x=y is labeled with 2 arrows that go to infinity in both directions.
This is misleading.
There should be a way to indicate that all points on this line remain fixed - maybe a different color ?
BTW. I only came across this type of degenerate phase portrait recently, in an electrical circuit in fact. This type does not appear in the book
"Differential Equations, Dynamical Systems, and Linear Algebra" (by Hirsch+Smale)
that I can see.
Thank you for pointing this out, Glenn! We have worked very hard to avoid this kind of edge case mistake, but we missed this one. Sharp eye! We'll get rid of the offending arrows. But I think the color stays red - all the trajectories in a given portrait have the same color.
Thanks again, and continue to enjoy the Mathlets!