Phase Lines
The nonlinear autonomous equation x' = g(x) can be understood in terms of the graph of g(x) or the phase line. As a parameter in g(x) varies, the critical points on the phase line describe a curve on the bifurcation plane.
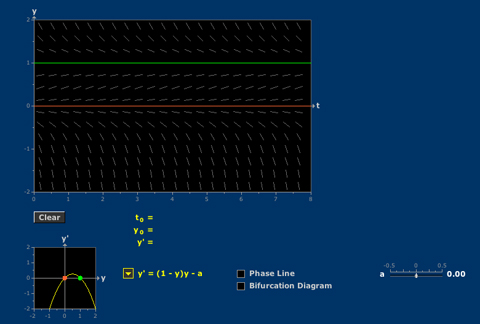 The nonlinear autonomous equation x' = g(x) can be understood in terms of the graph of g(x) or the phase line. As a parameter in g(x) varies, the critical points on the phase line describe a curve on the bifurcation plane.
The nonlinear autonomous equation x' = g(x) can be understood in terms of the graph of g(x) or the phase line. As a parameter in g(x) varies, the critical points on the phase line describe a curve on the bifurcation plane.
2 Responses to “Phase Lines”

This applet is absolutely beautiful! I relied extensively on it for introducing my first year undergraduate students to first order autonomous differential equations, and to basic nonlinear phenomena such as fold and pitchfork bifurcations.
According to me, an easy way to push even further the interest of the applet would be to add another equation. Indeed, one of the equations is y'=ay+y^3, it is the normal form of the pitchfork bifurcation in the subcritical case. It would be nice to add the normal form in the supercritical case, which reads y'=ay-y^3. Especially since the supercritical case is easier to connect to mechanics (buckling) and can also be related to the (supercritical) flip bifurcation occurring in the quadratic family (u_{n+1}=f(u_n) with f(u)=au(1-u)).
Thank you, Emmanuel, and especially thank you for the suggested addition to this Mathlet. We will implement it!