Matrix Vector
The product of a matrix and a vector depends in interesting ways on the entries of each. Eigenvectors represent a coincidence of direction.
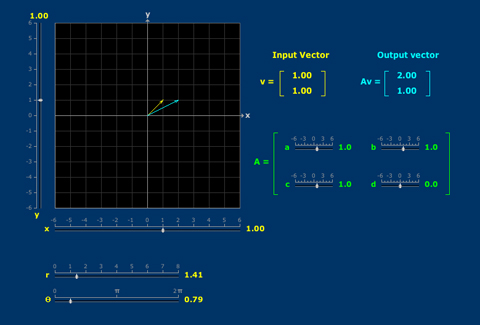 The product of a matrix and a vector depends in interesting ways on the entries of each. Eigenvectors represent a coincidence of direction.
The product of a matrix and a vector depends in interesting ways on the entries of each. Eigenvectors represent a coincidence of direction.
2 Responses to “Matrix Vector”

Very nice! I might suggest one additional display mode that may be helpful for building intuition, namely to display unit square bordered by the i and j basis vectors as inputs, and show how it is transformed into a parallelogram bounded by the column vectors of the matrix.
Thank you for this suggestion, David. This would make a good focus for a second Mathlet about 2x2 matrices. It seems slightly off topic for this one, which is really concentrating on eigenvectors. Maybe it's badly named!