Vector Fields
Nonlinear autonomous systems can have complicated solutions, which can be represented with some loss of information by their trajectories. Usually they behave nearly linearly near equlibria.
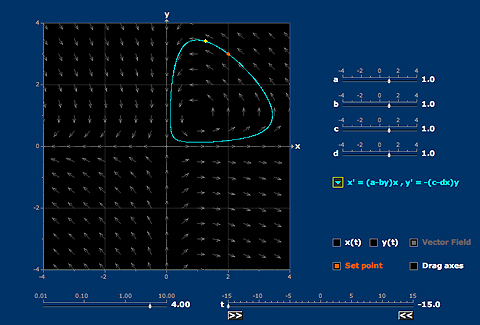Nonlinear autonomous systems can have complicated solutions, which can be represented with some loss of information by their trajectories. Usually they behave nearly linearly near equlibria.
One Response to “Vector Fields”
Thank you so much for this beautiful applet, which I extensively use to help my students grasp many fundamental ideas concerning vector fields and linear/nonlinear dynamics.
Here are a few suggestions concerning systems derived from second order equations (the last three systems in the list). [several suggestions omitted here but well noted!]
3 - A computation of the equation of the slow manifold (which is so clearly displayed when the damping parameter is large on the fourth and fifth vector fields) and the dynamics restricted to this slow manifold might be the subject of an interesting "activity".