Courses
Precalculus
- Affine Coordinate Changes
- Beats
- Beats with Sound
- Graphing Rational Functions
- Linear Programming
- Sinusoids
- Trigonometric Identity
Calculus
1. Differentiaton
- Amplitude and Phase: First Order
- Creating the Derivative
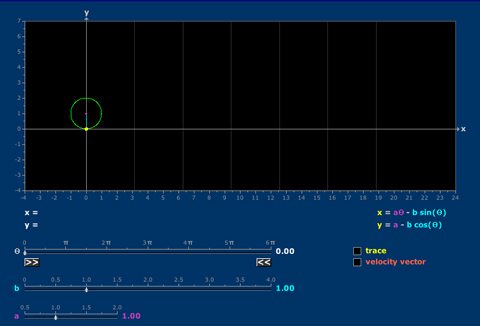
- Hypocycloids
- Secant Approximation
- Tangent Approximation
2. Higher derivatives
3. Integration
4. Vectors and matrices
Differential Equations
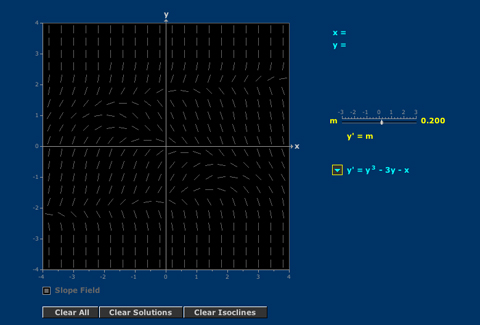
1. First order equations
2. More first order equations
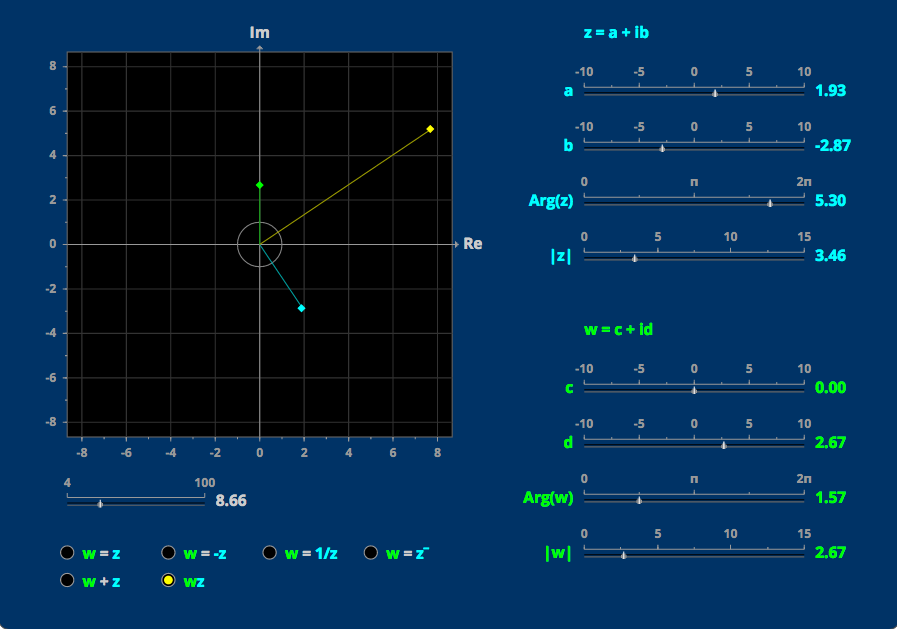
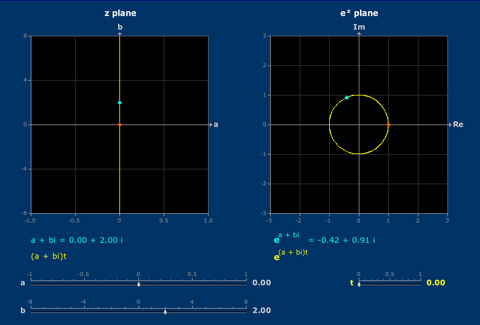
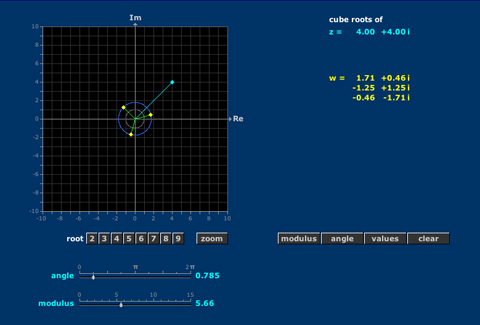
3. Complex Numbers
4. Second Order Linear Equations
- Amplitude and Phase: Second Order I
- Amplitude and Phase: Second Order II
- Amplitude and Phase: Second Order III
- Amplitude and Phase: Second Order IV
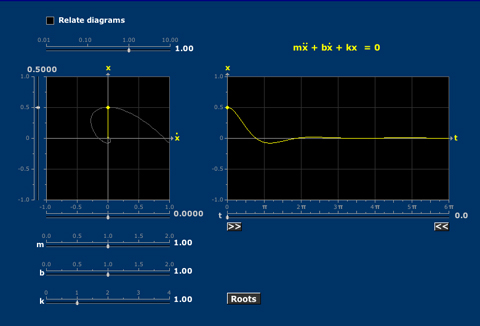
- Damped Vibrations
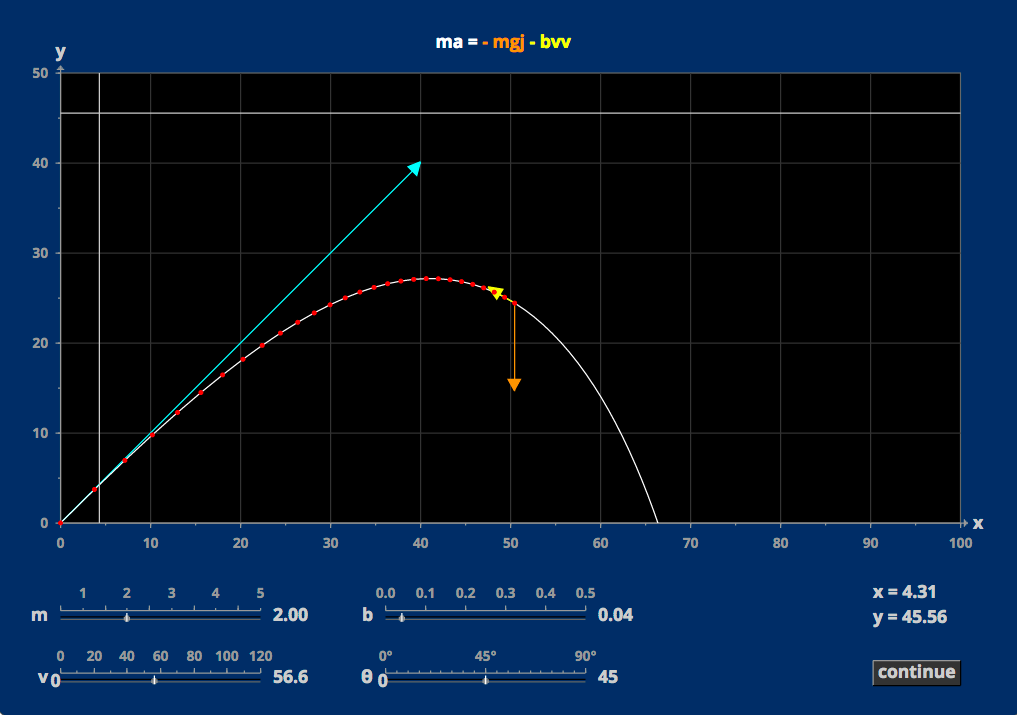
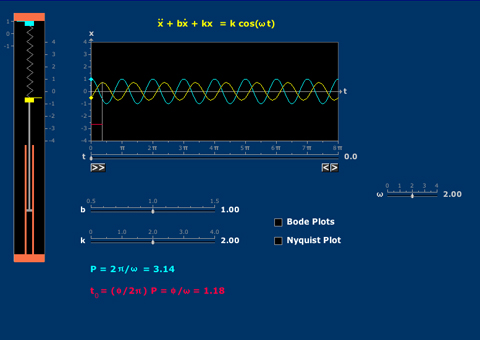
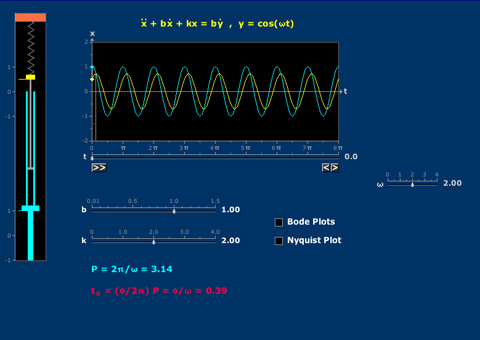
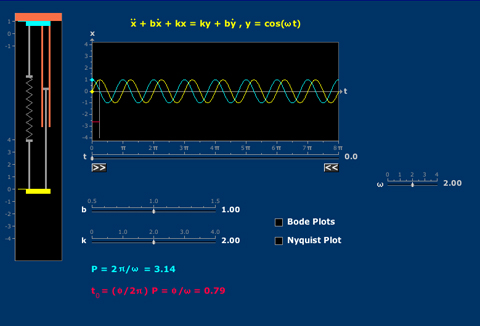
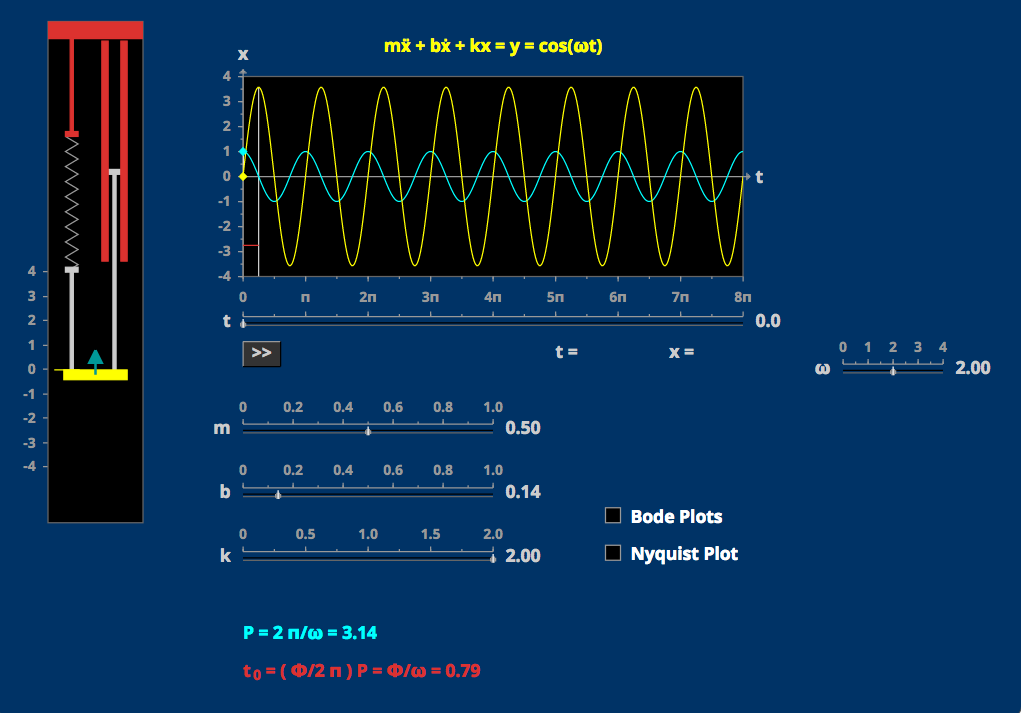
- Forced Damped Vibration
- Series RLC Circuit
- Sinusoids
5. Convolution, impulse response
6. Fourier series
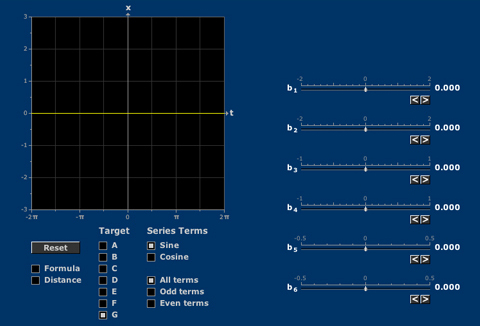
- Fourier Coefficients
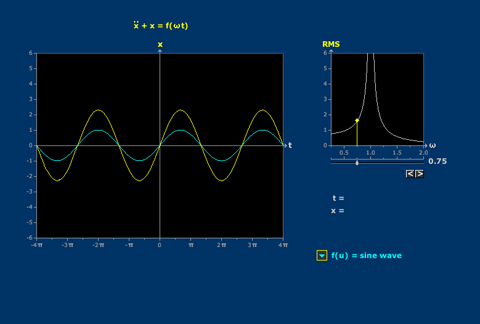
- Harmonic Frequency Response: Variable Input Frequency
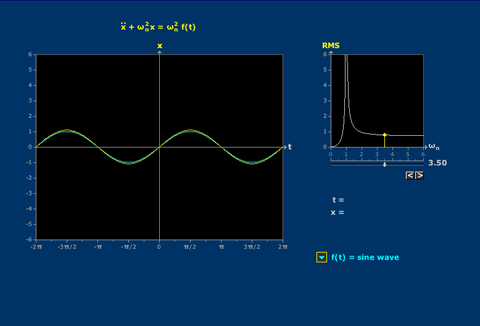
- Harmonic Frequency Response: Variable Natural Frequency
7. Laplace Transform
8. Linear systems
- Coupled Oscillators
- Linear Phase Portraits: Cursor Entry
- Linear Phase Portraits: Matrix Entry
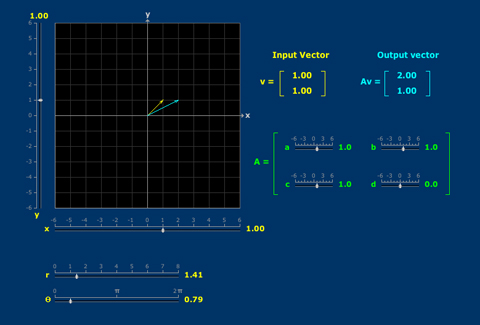
- Matrix Vector
9. Partial Differential Equations
Advanced applications of differential equations
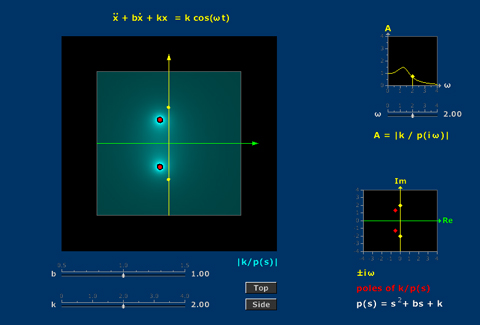
- Amplitude Response: Pole Diagram
- Bode and Nyquist Plots
- Damping Ratio
- Discrete Fourier Transform
- Fourier Coefficients: Complex with Sound
- Impulse Response: Spring System
- Series RLC Circuit
Probability and Statistics
- Beta Distribution
- Confidence Intervals
- Conjugate Priors
- Linear Regression
- Probability Distributions
- T Distribution